FAR model

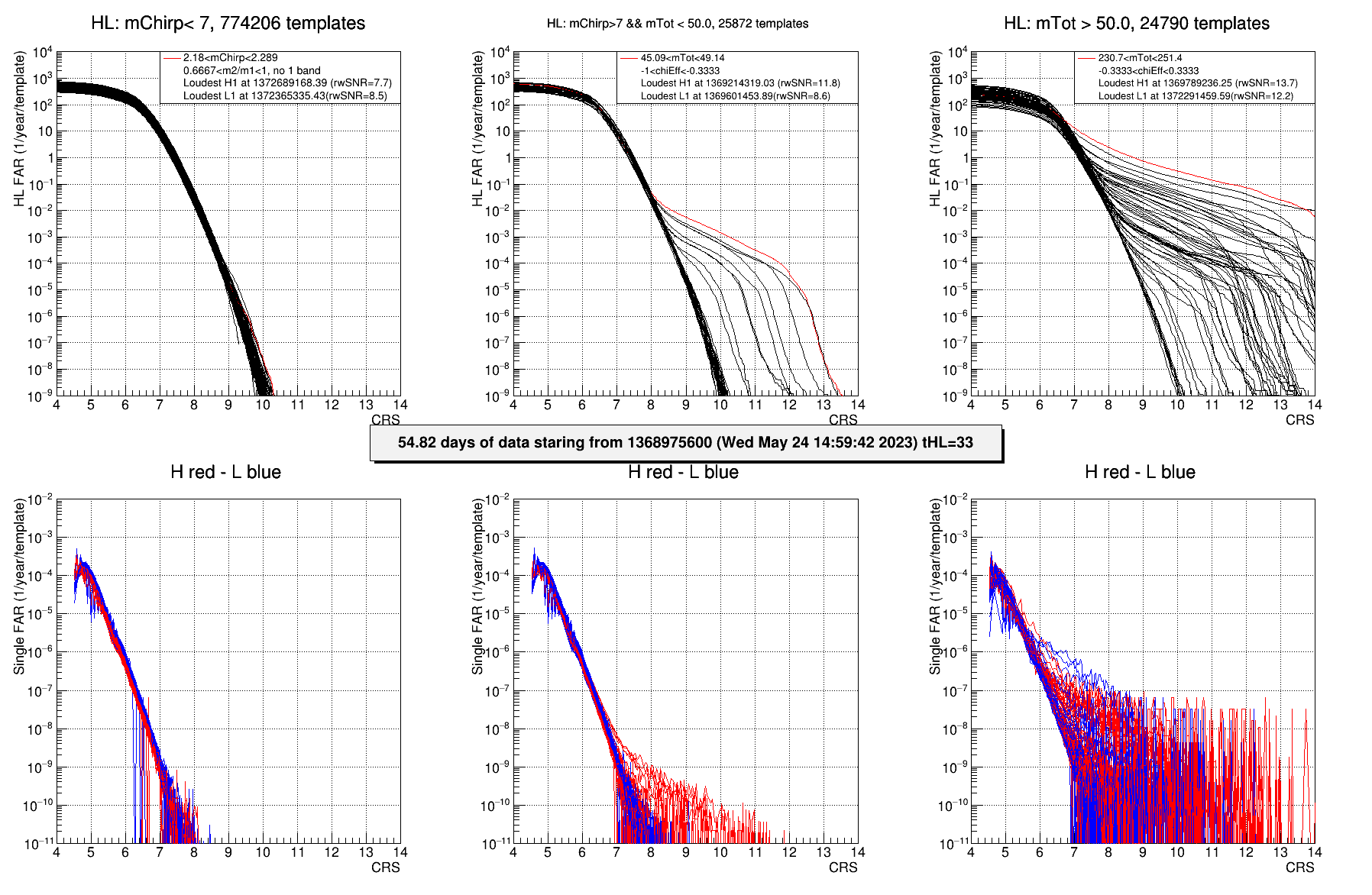
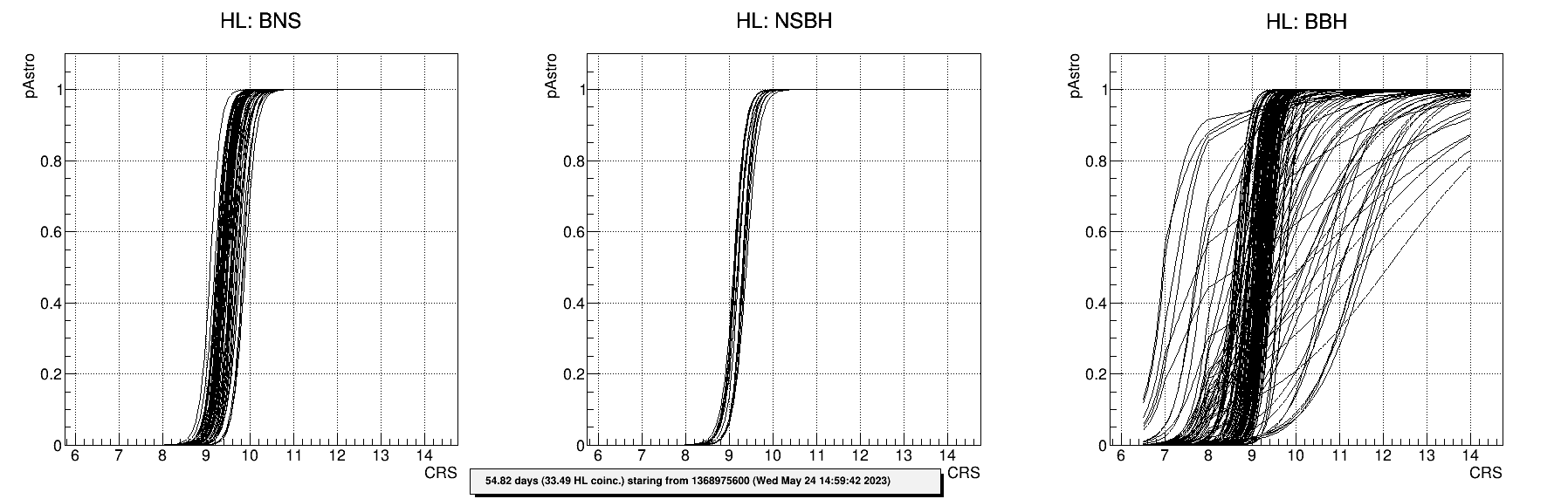
The false alarm rate and pastro for MBTA candidates are calculated in different 2-dimensional bins of the parameters space (see this technical note about the O4a template bank used by MBTA). For a chirp mass smaller than 7 solar masses, the binning is done using the variables chirp mass (43 bins) and mass ratio (3 bins), for larger chirp mass values, the binning is done using the variables total mass (40 bins) and effective spin (3 bins). For coincident triggers, and for each bin, we first build a FAR vs cRS model, by making all possible asynchronous random combination of single detector triggers from the same template obtained on data (before clustering, and excluding times around confirmed detections). The fit of the FAR vs CRS for each bin is shown in figure 2b.1 (top). We associate a FAR value to single-detector triggers only for possibly EM-bright sources (chirp mass smaller than 7 solar masses). To evaluate the FAR as a function of CRS for single-detector triggers, we accumulate background triggers (before clustering) using the same bins in parameters space as for coincidences (figure 2b.1 bottom).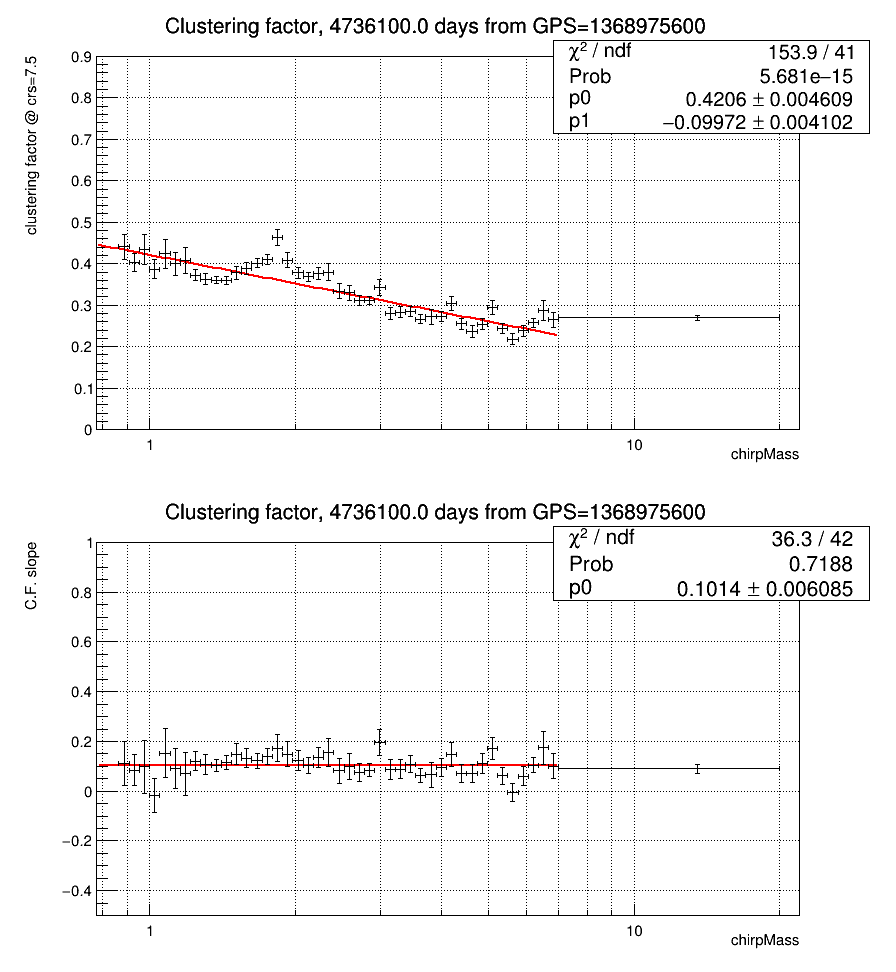

Fig 2b.1 : each curve represents the fit to the FAR distribution as a function of the combined ranking statistics, in one bin in chirp mass and mass ratio, in units (1/year) and per template (i.e. divided by the number of templates in the specific bin).

We then correct for the effect of clustering, and multiply the FAR value by the ratio between clustered and un-clustered triggers (the clustering factor). The clustering factor is found to depend linearly on the CRS and is determined with a fit in bins of chirp mass. The values of the constant and linear terms, as obtained from the fits, are shown in figure 2b.2, as a function of chirp mass (see here for more details on the fits for all bins). The values of the clustering factor parameters used to correct the FAR of MBTA candidates are determined by fitting their dependence on the chirp mass (red curves in figure 2b.2). In each bin, the FAR is extrapolated to higher CRS values by fitting the differential distribution of FAR vs CRS. The fit uses a piecewise function, allowing for (up to) a cubic dependence of log(FAR) on CRS at low CRS, and a linear one at high CRS (see here for more details on the fits for all bins) . In order to be conservative, for single-detector triggers the value of the slope for the high-CRS part is inflated by 5σ (see here for more details on the fits for single-detector triggers).

Fig 2b.2 : value of the constant term (for CRS=7.5, top) and slope (bottom) obtained by a fit to the ratio between clustered and un-clustered triggers (the clustering factor) in each chirp mass bin. The red curves are fits of the values as a function of the chirp mass, and represent the actual clustering factor applied to candidates.

Using the results of the MBTA search on data with overimposed injections (as provided by the rates and populations group), we evaluate the expected foreground contribution to each bin, for each source type (BNS, NSBH, BBH) and event type (HL, H, L, H-Lon, L-Hon). In each bin, we then evaluate p-astro (defined as the number of foreground expected events divided by the number of total events) as a function of the combined ranking statistics. The fits to the p-astro vs CRS distribution in each bin are shown in Figure 2b.3.

Fig 2b.3 : each curve represents the fit to the pastro distribution as a function of the combined ranking statistics, in one bin in chirp mass and mass ratio.

For each type of coincidence and for each source type, we combine the information on the FAR dependence on CRS and pastro dependence on CRS to get a FAR as a function of pastro, as shown in figure 2b.4 for HL coincidences, and figures 2b.5 and 2b.6 for single-detector triggers. The sum of false alarm rates for coincidences and singles, each weighted by the relative coincident/single livetime, is then normalised to the total observation time.

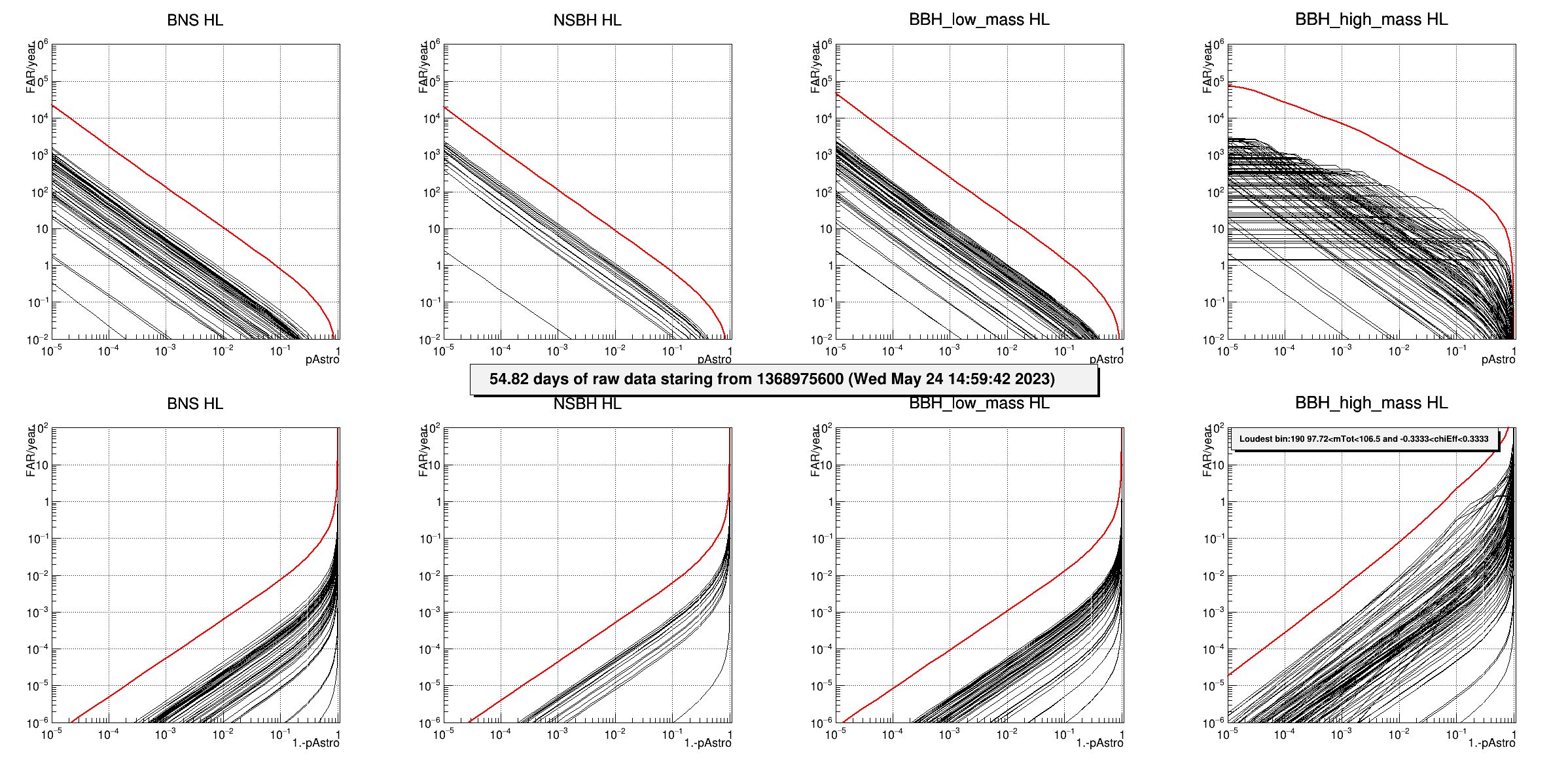
Fig 2b.4 : FAR (1/year) as a function of pastro for HL coincidences. The different pads show different regions in the parameters space and each black curve refers to a given bin (each bin is associated to the source type with the largest expected number of events). The red curve is the sum of all black curves and represents the final FAR per source type.

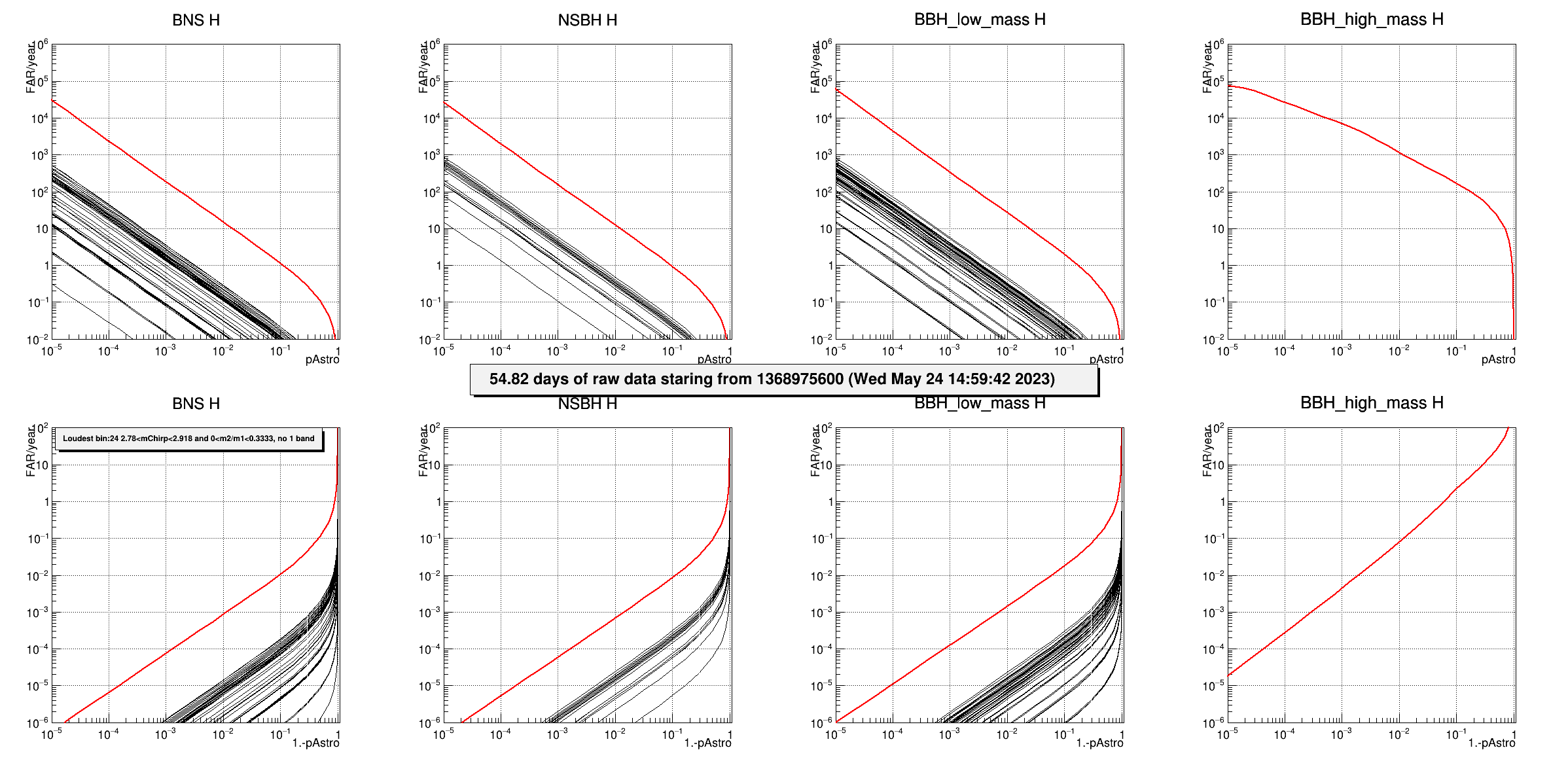
Fig 2b.5 : FAR (1/year) as a function of pastro for single-detector triggers in H. The different pads show different regions in the parameters space and each black curve refers to a given bin (each bin is associated to the source type with the largest expected number of events). The red curve is the sum of all black curves and represents the final FAR per source type.

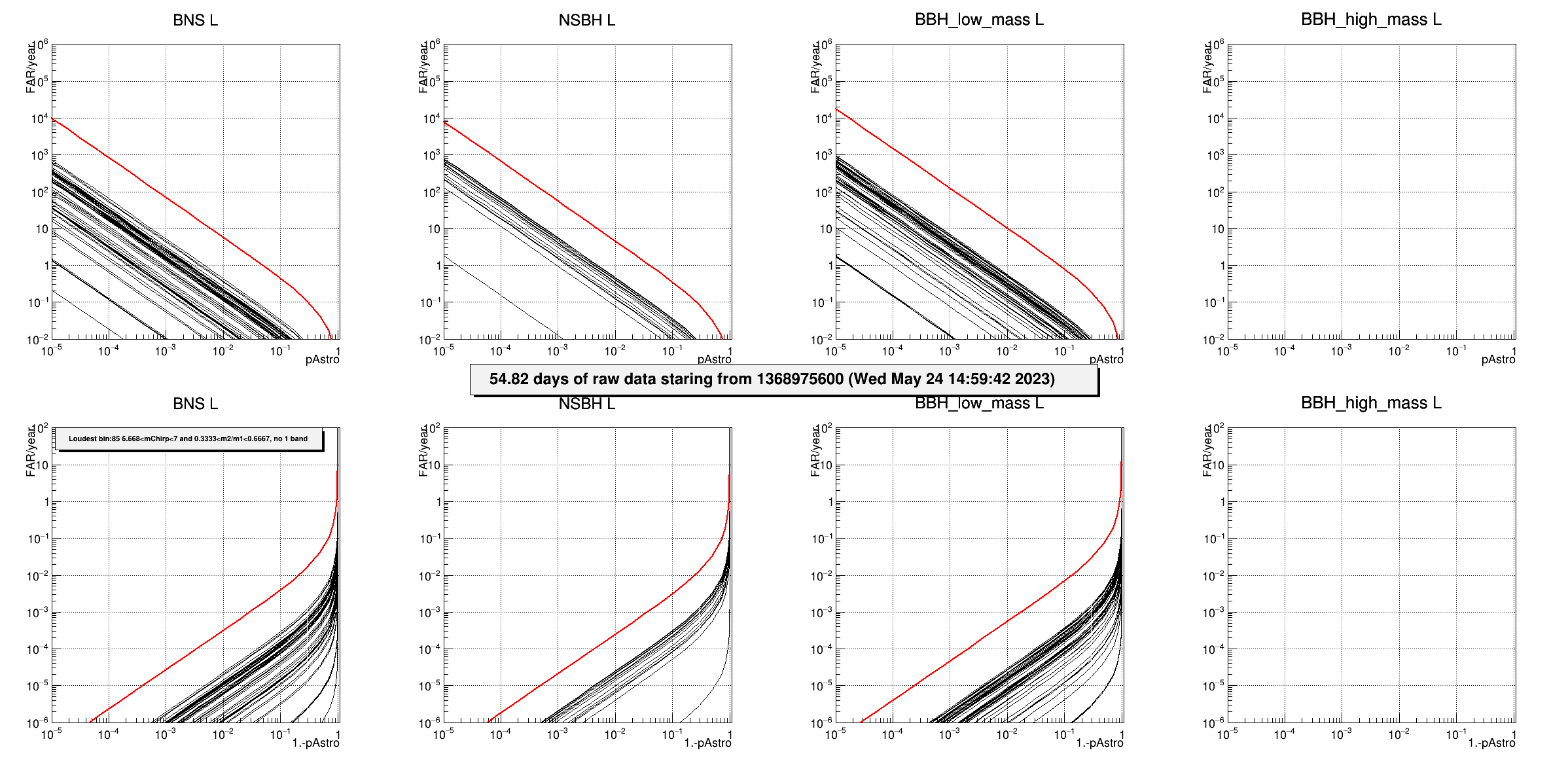
Fig 2b.6 : FAR (1/year) as a function of pastro for single-detector triggers in L. The different pads show different regions in the parameters space and each black curve refers to a given bin (each bin is associated to the source type with the largest expected number of events). The red curve is the sum of all black curves and represents the final FAR per source type.